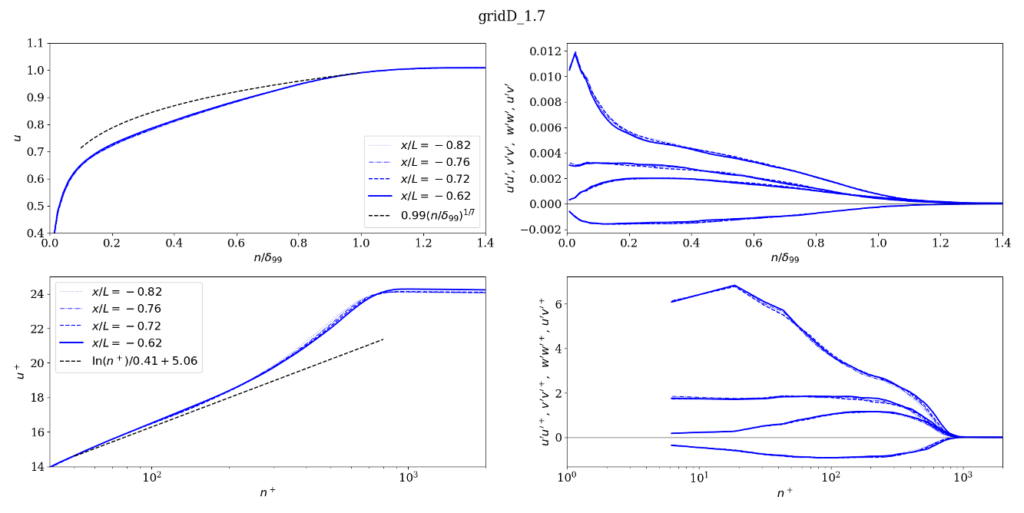
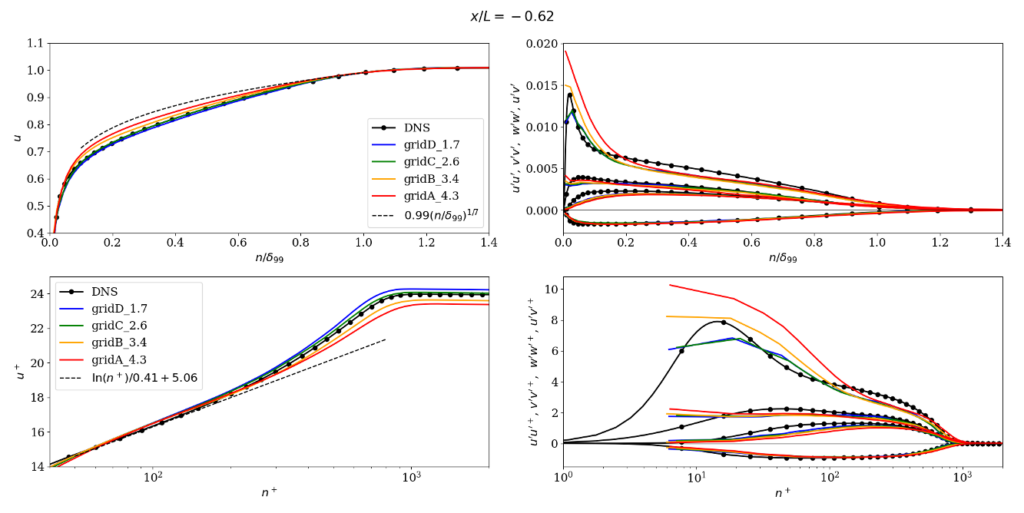
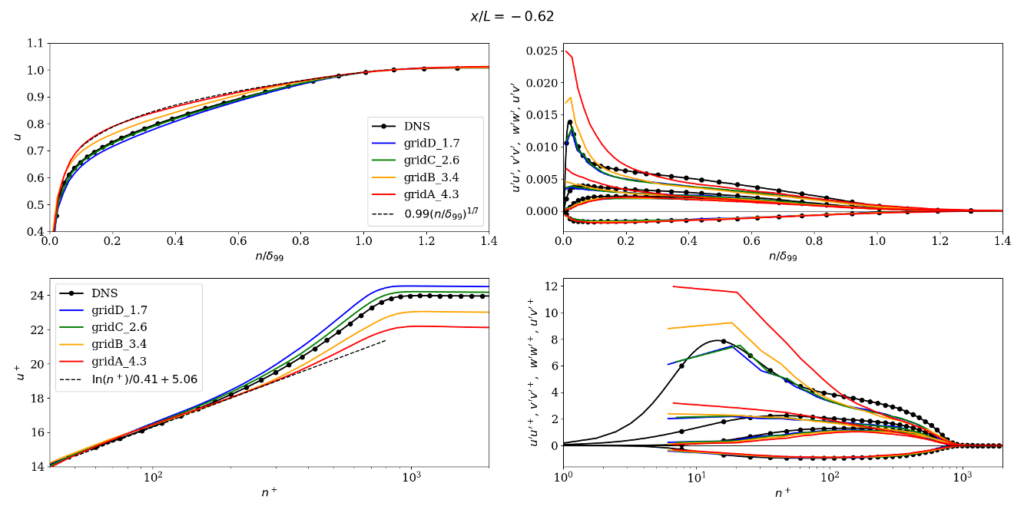
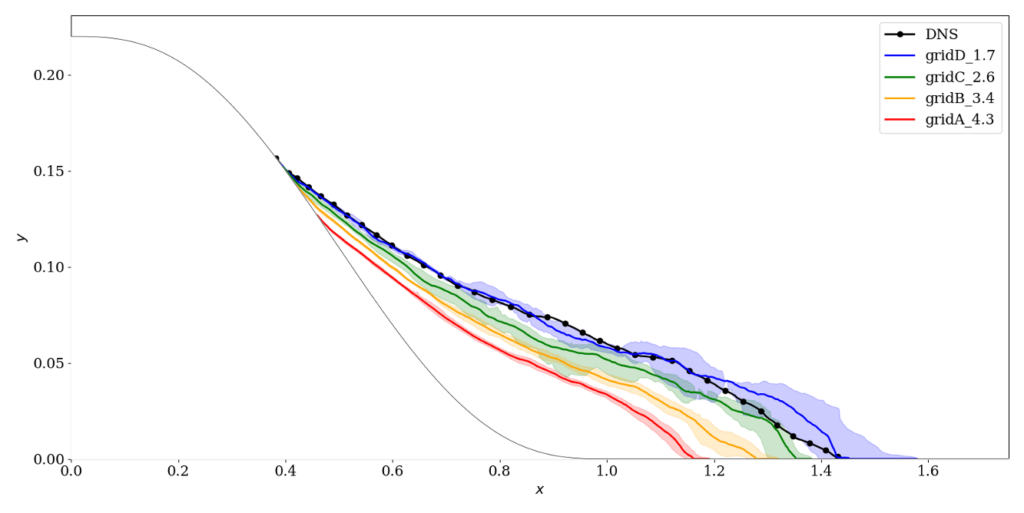
The results from the Tortuga::cLes solver developed in the Larsson group at the University of Maryland are shown here. This solver is a multi-block structured finite-volume code that solves the compressible Navier-Stokes equations using low-dissipation numerics that use face-based interpolation and differentiation stencils with 4 points; the code is formally 2nd-order accurate but with resolution properties typical of a 4th-order code. A standard equilibrium wall-model was used with exchange location fixed at \(h_{\rm wm} = 0.1 \delta_{\rm ref}\), with \(\delta_{\rm ref}/L=0.028\) taken from the incoming boundary layer in the reference DNS.
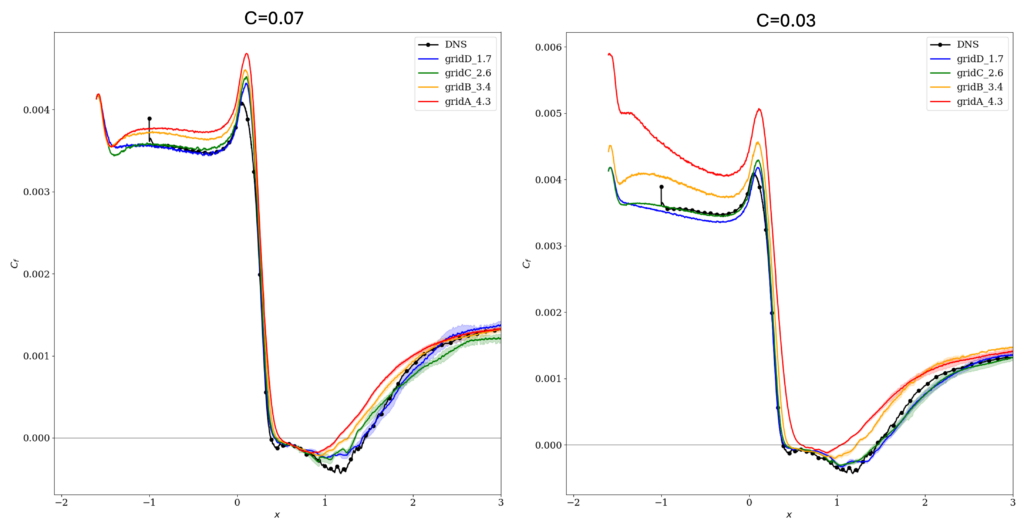
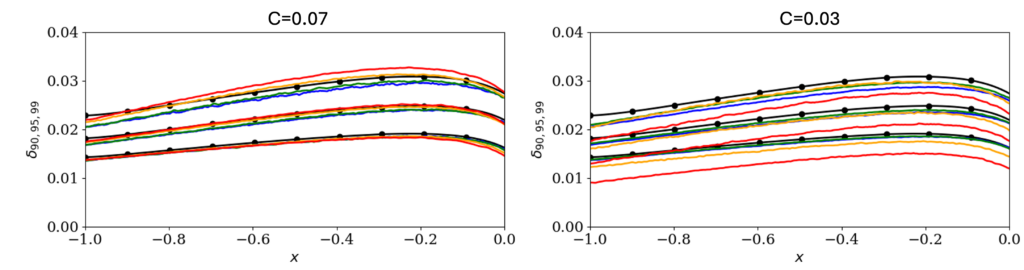
A Vreman subgrid model was used, with two different model coefficients of 0.07 and 0.03; this was done to test the sensitivity of the results to this parameter, and should not be viewed as saying anything about what the “optimal” coefficient might be, which will vary with numerics and other things.
The motivation of running these cases for the 2024 workshop was to test the basic method in general and an approach to structured grid-adaptation for LES in particular. As such, no attempts were made to find optimal code or model parameters to maximize accuracy for this case.
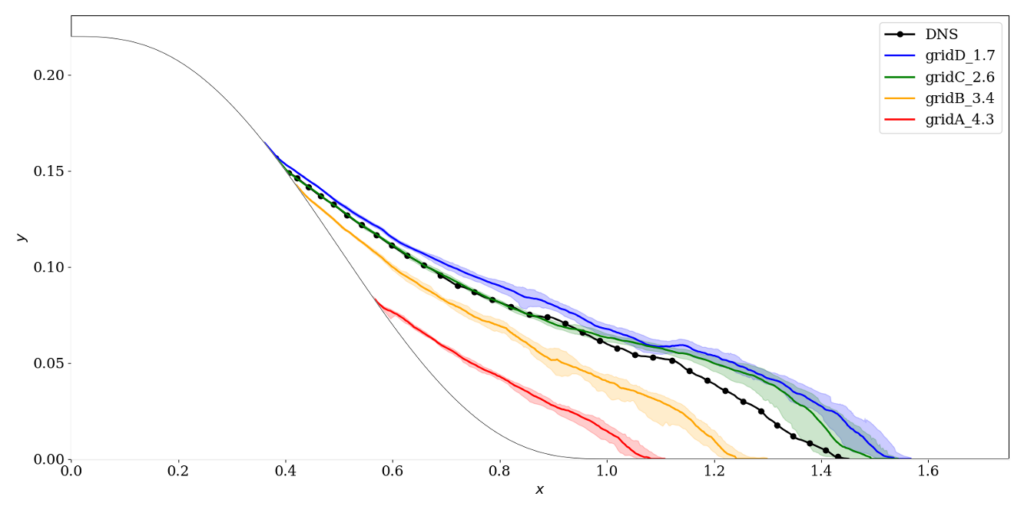
The coarsest grid (“gridA_4.3” in the results) was generated manually, and subsequent grids were generated automatically using the simple residual estimator of Toosi & Larsson (2017) and the grid-generation technique of Oberoi et al (to appear).
The full results considered at the 2024 workshop are available as pdfs for the model coefficient 0.07 and 0.03. Below are some key plots.