Turbulent channel flow is a basic validation problem for a WMLES approach. The periodic boundary conditions remove uncertainties and errors due to inflow turbulence, and the geometric simplicity means that one can easily run on a sequence of high-quality grids to really assess grid-convergence.
Basic set-up
We use the DNS by Lee and Moser (2015) as a validation case. The DNS is performed using the incompressible equations; in the results below, we have solved it at bulk Mach number of 0.2 using compressible solvers. The DNS was solved at specified bulk Reynolds number of \(Re_b = 125,000\), resulting in a friction Reynolds number of \(Re_\tau \approx 5200\). The domain used in the DNS was \((8\pi h, 2h, 3\pi h)\) in the streamwise, wall-normal and spanwise directions (where \(h\) is the channel half-width). Since the purpose here is to validate WMLES, we are only interested in the region immediately above the wall-model, say, for \(y/h \lesssim 0.5\). This near-wall region is less sensitive to the domain size, and we therefore use domans of size \((12.8h, 2h, 4.8h)\) here to reduce the number of grid points by about a factor of 4.
For wall-stress models we apply the wall-model over a layer of thickness \(h_{\rm wm}/h = 0.1\). For hybrid LES/RANS models, the thickness of the RANS layer is taken the same (i.e., the nominal location of the RANS-LES switch is placed at \(y = h_{\rm wm} = 0.1h\)).
Grids
We use grids at 4 different resolution levels in order to judge grid-convergence. The resolution level is quantified (and labeled) by the spanwise resolution \(\Delta z/h\): the 4 grids have \(\Delta z/h =\) 0.100, 0.067, 0.050, and 0.033.
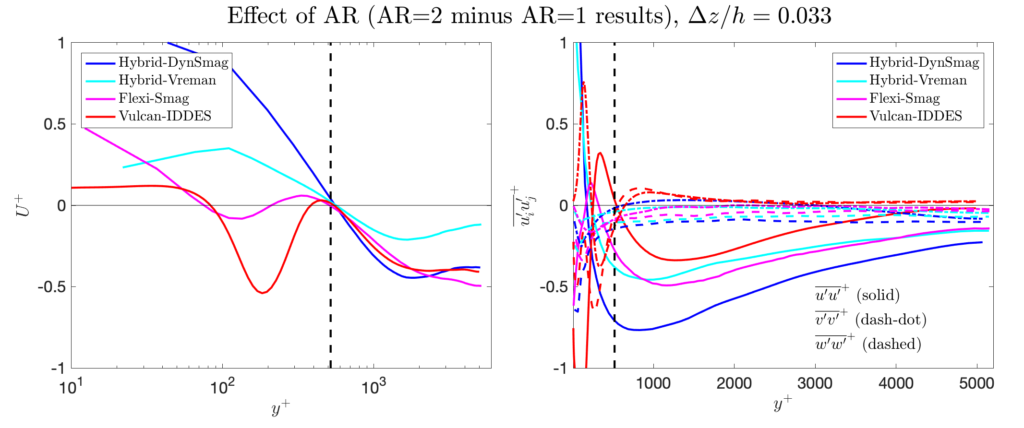
We use grids with 2 different aspect ratios in the wall-parallel plane in order to judge the sensitivity to the grid anisotropy. The base grid has \(\Delta x = \Delta z\) (which is consistent with the idea that one would not know the flow direction a priori for complex flow problems). Given the known sensitivity of LES to grid anisotropy (cf. Meyers and Sagaut, 2007), we also use grids with \(\Delta x = 2\Delta z\). While many (most?) channel flow studies using (WM)LES in the literature used a single \(\Delta x / \Delta z\) ratio and never varied it, it is crucial to appreciate the importance of assessing the sensitivity of a (WM)LES approach to the cell aspect ratio.
There are two versions of every grid: one intended for wall-stress models, one intended for hybrid LES/RANS models. The former have \(\Delta y_w \approx 0.25 \Delta y_c\) (subscripts \(w\) and \(c\) denote the wall and the centerline, respectively) and are refined uniformly and isotropically. The grids for hybrid LES/RANS have \(\Delta y_w / h= 1.5 \! \cdot \! 10^{-4}\) at all resolution levels; this value produces \(\Delta y^+_w \approx 0.8\) which is not refined in order to reduce the time-step penalty for compressible solvers. The wall-stress and hybrid LES/RANS grids have identical grid-spacings in the core 69% of the channel (i.e., for \(y/h \gtrsim 0.31\)). At the centerline, \(\Delta y_c = \Delta z\).
The actual grids can be downloaded from this separate page.
Results
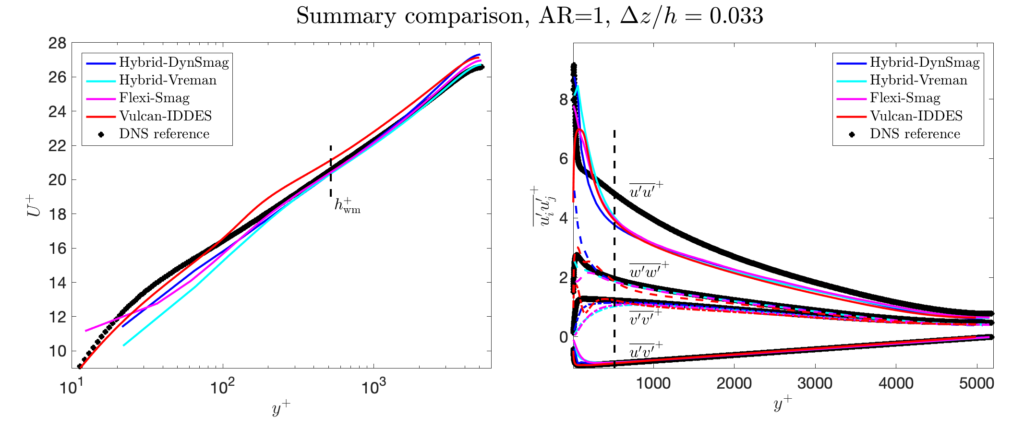
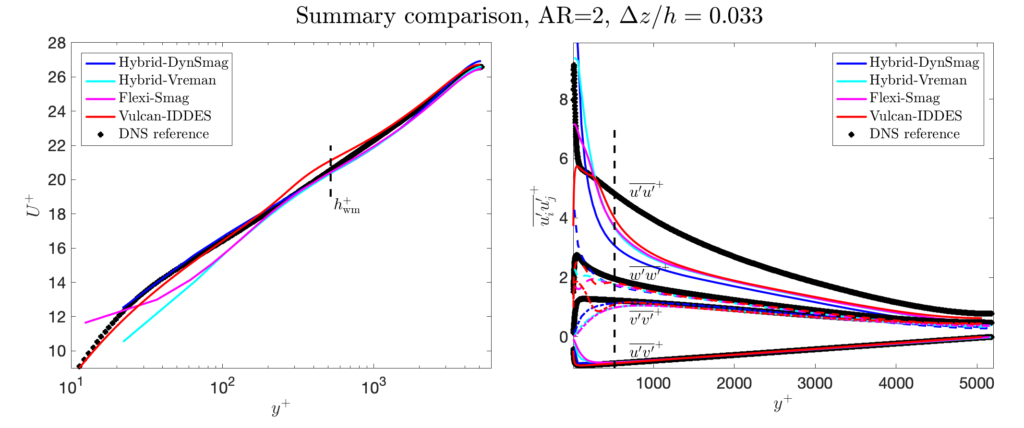
The results from some models are shown here to allow WMLES users a point of comparison with their own codes, models, and implementations. For every model, we have computed results on all grids. Before analyzing the results, it’s important to ask what one should be looking for (and what one should ignore)? Consider the following points:
- The chosen domain-size will affect the results in the core of the channel, specifically the “wake” of the mean velocity profile. Therefore, perfect agreement with the DNS should not be expected in the wake region. In addition, the smaller domain (compared to the DNS) presumably limits the formation of some “super-structures”, thus possibly causing the streamwise stress to be underpredicted compared to the DNS.
- The lower edge of the LES region (i.e., the location \(y=h_{\rm wm}\)) is marked by a dashed line in the figures. For wall-stress models, the results below this level are not meaningful, and should essentially be ignored (we show them anyway here to be transparent and complete). For hybrid LES/RANS models, the mean velocity below this level is meaningful, but the resolved stresses are not (and should essentially be ignored).
- When it comes to the grid aspect ratio AR (\(= \Delta x / \Delta z\)), the ideal result is (of course) that this should not affect the results at all. Since the spanwise grid-spacing \(\Delta z\) should be the limiting one for these problems, we show the difference in the results between grids with the same \(\Delta y\) and \(\Delta z\) spacings, but with different \(\Delta x\).
A summary comparison on the finest grids is shown below; the complete results for each model is shown in separate pages for each model. We currently have results for:
- The equilibrium wall-stress model, implemented in a minimally dissipative 6th-order accurate code (the Hybrid code, from JL’s research group at the University of Maryland) together with two different subgrid models: the dynamic Smagorinsky model (with filtering and averaging in wall-parallel planes), and the constant coefficient Vreman model (with coefficient 0.07).
- An equilibrium wall-stress model, implemented by iterative solution of the Spalding equation, in the Discontinuous Galerkin code Flexi (from the University of Stuttgart).
- IDDES (Menter-BSL) in the Vulcan code (from NASA Langley).